
K Nearest Neighbors Conceptual Understanding and Implementation in Python
K Nearest neighbors shortly know as KNN is a supervised algorithm which can be used for both Classification and Regression tasks. It is a simple and easy to implement algorithm.
Assumption
KNN algorithms assumes that all points that are similar are near to each other.
How it works?
- Compute the distance of new point with all points
- Sort the points based on the distance
- Choose majority among K nearest neighbors (K can vary from 1 to n)

From the above picture we can predict new point is a circle if k value is 5, because majority of the nearest neighbors are circles so we can easily classify it as a circle. Let’s see other case, in the below figure, try to predict the output for k value 5.

Generally, to identify the new label, first we will calculate the distance of new point with other points and sort the points based on the distance. We can easily sort first four points, but next three points have same distance, in order to get the fifth point, we must break the tie, these kinds of ties are called Distance Ties.
How to break the distance tie?
- Choose randomly and assign the label
- Consider all points which are equidistant and choose majority point and assign the label
In the above scenario if we choose randomly, we can either assign circle or star to the new point, but if we use majority than we can go with star. So, depends on the use case that we are solving we can go with such kind of approaches to break the tie.
Let’s see another scenario where we have another kind of tie call Voting tie.
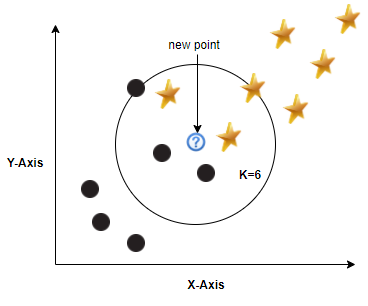
In the above figure for k=6 we have three circles and three stars as nearest neighbors, as count of both labels are same, we need to decide which label to go with. These kind of ties are called voting ties.
Below are some of the approaches to break the voting ties.
- Break the tie randomly.
- Break the tie using weighted voting (weight α 1/Euclidian distance).
- If you still have a tie than decrease the k value and choose the label.
How we choose k value?
- Small value of k influences the surrounding area drastically
- Large K values will always predict the majority label
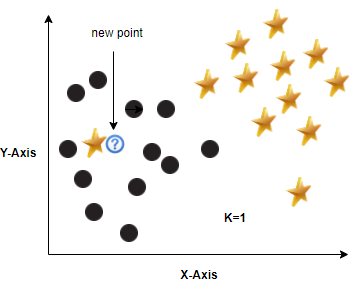

In the above figure we can clearly visualize that new point falls in to circle category but because of less k value we predicted it as a star, In other figure where k=2, here also since the k value is less we predicted incorrectly.

Now in this scenario see how larger k value impact the predictions. Here if you increase the k value after a certain threshold, the output prediction is always circle. Larger k values always predict the majority label. So, choosing the k value is very crucial in KNN algorithm.
We can choose k value by doing hyperparameter tuning. We will give wide range of k values and see how evaluation metric is changing if we increase the k value. In the below figure our evaluation metric is Accuracy and accuracy of model is more when the k value is 7. You can choose other evaluation metrics like Precision, Recall, F1 score as per the nature of the data and the importance of metric.

Another important step in KNN is distance calculation. Many ways we can calculate distance. Here we can go through some of the few important distance metrics.
Distance Metrics
Minkowski distance
Minkowski distance or Ln norm is a generalized distance metric. We can use below formula to calculate distance between two points in many ways

n= norm (any number).
xi,yi= ith data points of any number of dimensions.
k=number of dimensions.
We can change the distance of n and calculate the distance in three different ways.
Manhattan distance
If you want to calculate the distance between two data points in a grid like path than we use Manhattan distance. In the above formula just keep n=1 to calculate Manhattan distance

Here k is number of features.
xi,yi are features of vectors x and y respectively in two dimensional space i.e. x=(x1,x2,x3,….,xn) y=(y1,y2,y3,….,yn)

Euclidian Distance
It is one of the most used distance. We can calculate this by setting n=2 in Minkowski formula. This distance might not work in high dimensional spaces.

if x=(x1,x2,x3,..,xn) and y=(y1,y2,y3,..,yn) than distance is
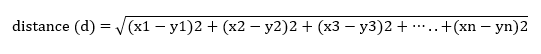
Chebyshev Distance
In Minkowski formula if n =∞ than we call it as Chebyshev Distance.
When n becomes large than the distance is nothing but the maximum value of the distance between the features.

Hyperparameters
K Value and Distance metrics
Advantages of KNN
- KNN is instance-based learning so it is called Lazy learning algorithm. It does not learn anything during the training period, and it will not create any prediction function from the training data. It stores the training dataset and k value and learns from it only at the time of making real time predictions. As there is no training time KNN algorithm is much faster than other algorithms.
- KNN can be used for both classification and Regression problems.
- As KNN algorithm don’t requires training, new data can be added continuously which will not impact the accuracy of the algorithm
- It is easy to implement as we have only two hyperparameters to tune and implement.
Disadvantages of KNN
- Does not work well with large datasets as the distance calculation of new point with other existing points is huge. It will degrade the performance of the algorithm.
- We need to do feature scaling before passing it to KNN for predictions as the range in magnitude has huge effect on distance calculation.
- Does not work best with high dimensions data because with large number of dimensions, calculating the distance in each dimension is difficult.
- KNN is sensitive to noise in the data, so we need to remove outliers and impute missing values.
Implementation of KNN using Python
Sample KNN algorithm implementation on open source breast cancer dataset using Python by Citrus is available in GitHub repo for reference.



